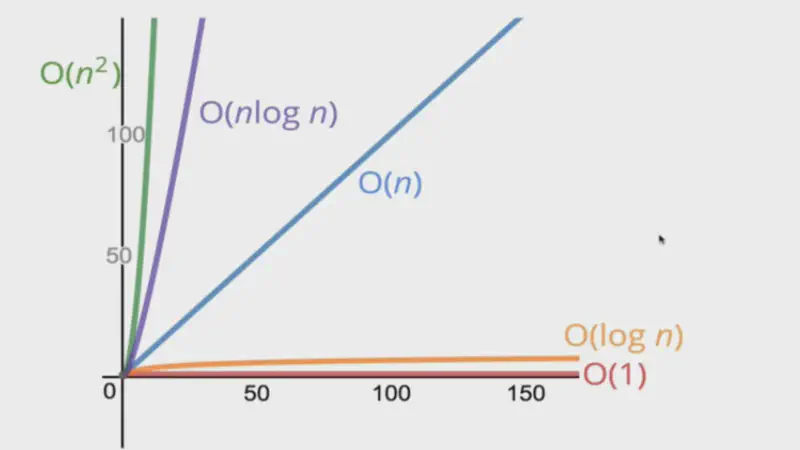
Time Complexity

Time Complexity o tiempo de ejecución es una medida de la cantidad de tiempo que un algoritmo necesita para ejecutarse. No se mide en segundos, sino en operaciones. Dicho de otra forma, es el saber cuántas operaciones primitivas son ejecutadas.

Cuando hablamos de time complexity, no pensamos en todos los pequeños detalles, sino que (generalmente) solamente queremos tener una estimación big picture, por lo tanto eliminamos o no obtenemos lo que se llama non-significant numbers, que es cualquier cosa que no es O(logn), O(n), O(n^2), O(k^n).

Si el data set es pequeño, es mejor centrarse en la legibilidad del código en lugar del performance

Quadratic time (n^2)

Un ejemplo es cuando cada número es comparado con todos los otros, usando nested loops.

Conforme nuestros datos crecen, el número de operaciones aumentan a la potencia de 2 (n^2).

Este es un ejemplo de Time Complexity.

Linear time (n)

Ejemplo: cuando queremos obtener el valor mínimo y máximo de un array, usando dos loops, pero no anidados.

¿Cuántas comparaciones se hacen?

Para el primer loop, se hacen n comparaciones, donde n es el tamaño del array. Para el segundo loop, también se hacen n comparaciones.

Entonces, la complejidad de nuestro algoritmo es 2n (hay que recordar que nuestros loops no estaban anidados).

Conforme nuestros datos crecen, el número de operaciones aumentan a por 2.

Constant time (1)

Imaginemos que tenemos un array de números, este array ya está ordenado, y queremos obtener el valor mínimo y máximo.

¿Cuántas comparaciones se hacen?

Para obtener el valor mínimo, solo necesitamos obtener el primer valor, lo que sería una operación.

Para obtener el valor máximo, solo necesitamos obtener el ultimo valor, lo que sería una operación.

Esto nos deja una complejidad de 2.

Logarithmic time (log n)

Conforme nuestros datos crecen, el número de operaciones que se requiere hacer, disminuye por una fracción.

Un ejemplo de esto es cuando se hace un loop sobre un array, y cada vez que se hace el loop, cortas el problema a la mitad (o alguna fracción. Base 2 divida por 2, base 3 dividida por 3…).

Big-O Notation de más rápido a más lento

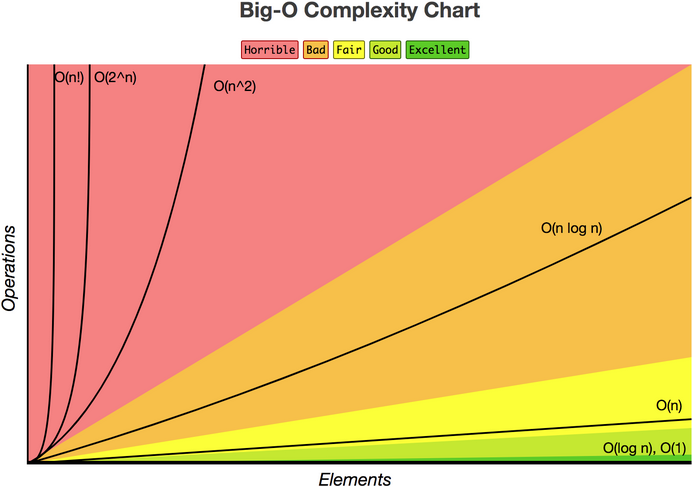
Complejidad de expresiones comunes

Métodos y expresiones de JS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

const arr = [1,2,3,4,5];
arr.pop(); // O(1) - constant
arr[0]; // O(1) - constant
arr.shift(); // O(n) - linear

// ----------------------------

const obj = {a: 1, b: 2, c: 3};
obj.a; // O(1) - constant

// ----------------------------
1 + 1; // O(1) - constant
1 > 2; // O(1) - constant
1 < 2; // O(1) - constant

.shift es linear porque hay que mover todos los elementos una posición a la izquierda.

.forEach y .map son métodos solo loops, el problema viene en el callback, este puede elevar la complejidad del algoritmo.

Ejemplo

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

function getTotalChars(word) {
  let total = 0; // O(1) - constant
  for (let i = 0; i < word.length; i++) {
    total++; // O(n) - linear
  }
  return total; // O(1) - constant
}

getTotalChars('hola'); // O(n) - linear
getTotalChars('estapalabraesmuylarga'); // O(n) - linear

// ----------------------------

function getTotalChars(word) {
  return word.length(); // O(1) - constant
}

getTotalChars('hola'); // O(1) - constant
getTotalChars('estapalabraesmuylarga'); // O(1) - constant

Space Complexity

Space Complexity es una medida de la cantidad de espacio que un algoritmo usa.

Si el algoritmo copia un array cierta cantidad de veces, entonces en memoria tienes cierta cantidad de arrays, entonces tienes cierta cantidad de space complexity.

Funciona con las mismas medidas que time complexity, pero en lugar del número de operaciones, pensamos en la cantidad de espacio que usa el algoritmo.

Ejemplos obtenidos de Bianca Gandolfo